卷积计算器

输入第一个数据序列:

1 1 1 0 0 0

输入第二个数据序列:

0.5 0.2 0.3

计算 重置

数据结果序列:

卷积计算

序列 y(n) 等于序列 x(n) 和 h(n) 的卷积：

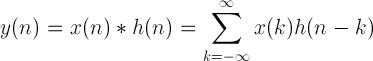
对于具有 M 值的有限序列 x(n) 和具有 H 值的 h(n)：

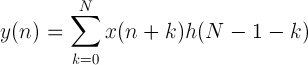
对于 N = 0 .. M+H-2

卷积是 f(τ) 与反向函数 g(t-τ) 的相关函数。

卷积运算符是星号*。

• 连续卷积
• 离散卷积
• 二维离散卷积
• 卷积滤波器实现
• 卷积定理

连续卷积

f(t) 和 g(t) 的卷积等于 f(τ) 乘以 f(t-τ) 的积分：

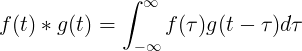
离散卷积

2 个离散函数的卷积定义为：

二维离散卷积

二维离散卷积通常用于图像处理。

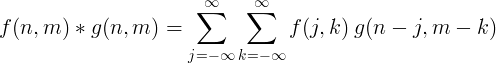
卷积滤波器实现

我们可以通过与脉冲响应 h(n) 的卷积对离散输入信号 x(n) 进行滤波，得到输出信号 y(n)。

y ( n ) = x ( n ) * h ( n )

卷积定理

两个函数相乘的傅里叶变换等于每个函数的傅里叶变换的卷积：

ℱ{ f  ⋅ g } = ℱ{ f } * ℱ{ g }

2 个函数卷积的傅里叶变换等于每个函数的傅里叶变换的乘积：

ℱ{ f  * g } = ℱ{ f } ⋅ ℱ{ g }

 

连续傅里叶变换的卷积定理

ℱ{ f ( t ) ⋅ g ( t )} = ℱ{ f ( t )} * ℱ{ g ( t )} = F ( ω ) * G ( ω )

ℱ{ f ( t ) * g ( t )} = ℱ{ f ( t )} ⋅ ℱ{ g ( t )} = F ( ω ) ⋅ G ( ω )

离散傅里叶变换的卷积定理

ℱ{ f ( n ) ⋅ g ( n )} = ℱ{ f ( n )} * ℱ{ g ( n )} = F ( k ) * G ( k )

ℱ{ f ( n ) * g ( n )} = ℱ{ f ( n )} ⋅ ℱ{ g ( n )} = F ( k ) ⋅ G ( k )

拉普拉斯变换的卷积定理

ℒ{ f ( t ) * g ( t )} = ℒ{ f ( t )} ⋅ ℒ{ g ( t )} = F ( s ) ⋅ G ( s )